Biography
Vita
Publications
Books
Images
Videos
Genealogy Professional
Hobbies
Nat’s Medal Science

Biography

Generously contributed by Michael H. Freedman.

Family
Youth
1973-75 in Berkeley
Topological 4-manifolds
Exotic R⁴‘s
Awards
The in-between years, 1982-1997
A quantum computer
Microsoft and Station Q
Miscellany
References

Mike’s family

Mike Freednam was born in Los Angeles on 21 April 1951, to Nancy Mars Freedman and Benedict
Freedman. Ben’s father, David, was born in Romania and emigrated to New York, where he became a
major writer of comedy sketches for radio and Broadway shows, in particular, the Ziegfield Follies, Burns
and Allen, Eddie Cantor, and Fanny Brice. He died early in 1936, when Ben was 16.

Ben’s mother, Beatrice, was a formidable woman, and believed that Ben would be wasting his time in
part B of a course with two parts, expecting Ben to learn it all in part A. Consequently, Ben finished
Townsend Harris High School at the age of 13 and started Columbia in fall 1933. Beatrice’s determination
worked even better for a younger son, David Noel Freedman, who finished high school at 12 and went on
to be a distinguished professor in Biblical Studies, but not so well for youngest son Toby Freedman who
only finished high school at 16. “Toby the dope”, as his mother affectionately called him, played football
at UC Berkeley, got an MD from Stanford Medical School, and became the team physician for the Los
Angeles Rams and LA Lakers.

During 1933-34, Kurt Gödel was lecturing on his famous work in logic at the Institute of Advanced
Study, where Alonzo Church and two of his graduate students, Stephen Kleene and Barkley Rosser, were
listeners. Rosser came weekly to Columbia to report on Gödel’s lectures, and freshman Ben, even at his
age, was a serious participant, although he only returned to logic decades later.

In high school, Ben had learned quite a bit of math (in particular, calculus of finite differences). When
Ben’s father died, he left school and started working for an actuary, and writing comedy sketches. He met
Nancy, a dancer, actress and writer, and they were married in 1941, a marriage perhaps hastened because
Nancy had bacterial endocarditis and was given only months to live.

The newlyweds moved to Hollywood and continued to write scripts. At first, Ben was not drafted owing
to poor vision but, as World War II grew, he took a job as draftsman with Curtiss-Wright Aviation. When
the other draftsmen were drafted, Ben was promoted to teaching aeronautical engineering, relying on
his early math background. He shortly ended up with Hughes Aircraft, involved in building the famous
plywood airplane, the Spruce Goose. His skill with calculus of finite differences was valuable in building
a plywood plane, for plywood was inherently discrete, whereas regular calculus was appropriate for metal
planes.

An anecdote from those days involves Ben’s boss waking him up at 2 AM on the phone, telling him to take
two showers and to meet him and Howard Hughes at the airfield. Ben did so, a small plane arrived and
out stepped Hughes, who commanded Ben to remain at a distance (Hughes was famously germophobic).
Hughes said that he had a secret job for Ben, doubling his salary, but Ben could not tell anyone where he
was, although mail would be delivered to and from Ben. Ben said he couldn’t leave Nancy for the war
nor for Hughes, so there ended that bizarre episode.

Ben and Nancy continued to write, and in 1947 published their first novel, Mrs. Mike, a best seller about
a teenage girl who went to live in northern Canada in the 1800s. Ben wrote scripts for the Red Skeleton
Show for 12 years, and for Mickey Rooney movies, such as Atomic Kid and Hatari; he still enjoyed
doing math in his spare time. In 1965, he went back to school at UCLA, obtaining a Ph.D. in logic under
Yiannis Moschovakis in 1970. He taught at Occidental College until his retirement. Nancy died in 2010.

Mike has two sisters: Johanna, who has a PhD in psychology from Stanford and is a professor at UC
Irvine Medical School (where she directs a program in the medical humanities and the arts), and Deborah,
who is an opera singer and teaches voice, sometimes at UC Berkeley.
Mike has four sons, three with his wife Leslie (Sam) Howland; the sons have tough acts to follow.

Mike’s youth

Mike’s father (in 2011) recalls with a scriptwriter’s gift this next picture of Mike as a teenager, which
nicely captures the Mike we know as an adult:

Mike and Doug tackle El Capitan
by Benedict Freedman

Mike was fifteen and in Pali High (Pacific Palisades, CA, a Los Angeles suburb overlooking the Pacific).
We had a pool, and he learned to swim at the age of 2, becoming a strong swimmer with superior
endurance. He never liked team sports, but got his exercise hiking through the hills of the Santa Monica
Mountains with his dog Rex. Being already a mathematician, his route was generally a geodesic, which
gave him some training in rock climbing.

At Pali High, he tried out for and made the swimming team, but always came down with a cold just
before the meet. He quit, and resumed his solitary hikes with Rex. Then, he found another loner of his
age, Doug McKenzie, and they teamed up.

After a few weeks of trudging through the hills, falling off boulders, and being cut to ribbons by the
brush, they decided that this was their true vocation. They bought ropes, pitons, carabiners – the whole
works. They went back into the hills and looked around for cliffs to conquer. They came home hours
after dinner, and ignored their homework. It had no effect on their grades; they already knew everything
high school had to teach them.

When they thought they were ready, they approached their parents with a plan. They would have their
drivers’ licenses in a few weeks, drive north to Yosemite, and after a few practice ascents climb El
Capitan by one of the easier routes.

Mrs. McKenzie, who had done some rock climbing herself, dismissed the whole project as absurd,
impossible, and definitely calculated to get them killed. Nancy and I, who knew nothing of rock climbing
and had never been to Yosemite, thought it a reasonable plan that might succeed a couple of years down
the road.

Mrs. McKenzie called on her husband for reinforcement, and they laid down the law: forget the whole
thing.

I don’t know how Doug responded, but Nancy and I realized it was a year too late to take that line with
Mike. He’d spent the summer before at UC Berkeley under a special program in mathematics for brilliant
high-school students. When he came home, he announced that he was now an adult, and would no longer
check in before midnight or reveal whom he was dating. In fact, next time he was at Berkeley, he might
never come back.

To which Nancy replied with a straight face, “If that’s what you want, Mike. We’ll miss you. Anytime
you’re in the neighborhood, drop in.”

Meanwhile, Mrs. McKenzie had come up with a compromise solution. She had located a young man
with Yosemite-climbing experience, who had gone into business tutoring amateurs on the basics. We
hired him, and he went along with the boys and the dog into the hills, for an overnighter. When they
returned, Mike reported, “He’s not a bad guy. He knows a few things, and really loves the Sierras. But he
keeps telling the same joke over and over, and like Dad says, ‘If it ain’t funny the first time, it ain’t funny
the fifth time.’ Also, he’s on drugs and lost his edge. Doug and I had to save his neck a couple of times.”
We gave in. But extracted a promise they would study the theory of climbing the way you learn any
scientific discipline, and test it in practice the way scientists test their theories. I bought a couple of books
to get started on.

They took me seriously and camped out in our big eucalyptus to hone their skills. They conceived the
idea of hauling Rex up into the tree and improving his education, thereby improving theirs. It says
something about human vs. animal cognitive abilities that Rex made the fastest progress, at least in
eucalyptus ascents. It was fascinating to watch the expression on the face of a cat who thought he had
escaped scot-free, and then saw this super-dog coming up the tree right after him.

To cut the story short, within the year they did climb El Cap. Nancy and I didn’t get particularly excited –
Mike had said they would do it, and they did it. But, several years later, en route to a writers’ conference
in Bishop, we took the long way through Yosemite and came unexpectedly on a little sign on the side of
the road. I stopped the car. “Look, Nancy, that’s El Cap.” She nearly fainted.

Mike became, and still is, an excellent rock climber, but stories of his exploits appear elsewhere.
During high school, Mike had a real interest in painting, picking up an expressionist perspective from his
mother. He took a batch of paintings (mostly watercolors) to college with him, but the idea of becoming
a painter soon disappeared.

Mike started college at UC Berkeley in 1968. He thought, perhaps incorrectly, that he knew enough
Calculus already, and skipped the lower-division math courses. He enrolled in an abstract algebra course,
a course in logic given by Michel Mendès from France, the son of the one-time French Prime Minister,
and courses in botany and French. His difficulty with the latter convinced him to try for graduate school
at Princeton after just one year.

Ed Nelson tells this story about Mike’s admission to Princeton graduate school:

Here’s the unvarnished tale. As always, Fox was chairman of the admissions committee. We
had finished making our list of acceptances, when a slightly late application came in from Mike.

I looked through the folder and it looked very good, so I took it to Fox to show it to him. Mike
had included a photo of himself standing on the top of a peak. That was a no-no at that time,
since a photo would reveal the applicant’s race. I started to show the folder to Fox, but he saw
the photo and said “admit him.” Just to be completely explicit, the photo is the only thing in the
folder Fox looked at. Honest, that’s what happened.

Mike drove across country to Princeton with a copy of Hoffman and Kunze propped up on the steering
wheel – he figured he ought to know some linear algebra before arriving. At Princeton, at the opening
lecture of Donald Spencer’s class on elliptic PDEs, he heard Spencer’s first sentence: “Let
S be the sheaf of germs of sections of a vector bundle. . . ” Well, he thought, at least I know what a vector is!

Despite the gaps in his knowledge, Mike finished a good thesis with Bill Browder in just four years, and
moved on to a postdoc at UC Berkeley in 1973.

1973-75 in Berkeley

Mike spent the academic years 1973-75 at UC Berkeley as a Lecturer (the name for our postdocs in those
days). I knew him slightly from climbing with him near Princeton when he was a graduate student, and
we continued to climb together when he was here. The next story is from that period.

A bouldering championship

Many of us have watched Mike climbing buildings, called “buildering,” or climbing boulders (bouldering),
or joined him on trips of greater magnitude. I had the privilege of joining him and Dennis Johnson on a
four-day ascent of the classic route on the northwest face of the Half Dome in Yosemite Valley. This was
in July 1975, only 18 years after the first ascent (in five days) by Royal Robbins, Mike Sherrick and Jerry
Gallwas in 1957, the first grade VI climb in the world.

It’s clear that Mike was a star climber among mathematicians, but how did he rank among the pros? This
following story offers some evidence.

The Great Western Bouldering Championship was held on Mike’s birthday, 21 April 1979, just south of
Mount Woodson in Southern California. The area is covered with many granite boulders, up to 100 feet
high. A committee chose a few dozen routes on these boulders, none more than 17-feet high, for ropes
were not used. The committee graded them, with the most difficult worth 22 points, the next 18 points,
and then several in the 17s, 16s and 15s. Each climber in the competition had to climb ten routes, and
received either zero or the grade of the climb if they were successful. Once both feet left the ground, it
was all or nothing.

Among the contestants was John Bachar, already one of the most famous climbers in the world, with
legendary feats of free, solo climbing in Yosemite. As the day went by, the best climbers, including
Bachar, had done nine climbs with similar total scores, but the two hardest climbs were still untried. As
daylight waned and the organizers got antsy, Mike attempted to organize a lottery, with the odd-man
out having to try a hard climb first, thereby perhaps giving away information about the difficult parts.
Mike was not successful, and gradually the other climbers drifted away and finished with easier climbs.
But not Mike, who gave the 18-pointer a try, and of course succeeded and won the Championship. Why
didn’t Bachar try? Perhaps he was not as inclined as Mike to try “hard problems”!

Now, it was up to Mike to see if he could become a better mathematician than a climber, and he did so in
late August 1981.

I had heard Andrew Casson give a talk about another, simpler proof of Rokhlin’s Theorem, that a spin,
closed, smooth 4-manifold had to have signature (index) divisible by 16, not just 8. I recounted Casson’s
proof in a seminar in Berkeley, and afterward Mike and I talked about the proof. My recollection is that
he was the driving force in coming up with the argument that appears in our joint paper [1978], and that
he did most of the writing (Mike gets math written up quickly, the opposite of me). The arguments in that
paper led me to further work, and eventually to the proof of Rokhlin’s Theorem (and its extensions) in
my book, The topology of 4-manifolds [1989], which I consider the right way to prove the theorem. This
was a fine collaboration in all respects, from my point of view!

In spring 1974, I spent 3 months at IHES, and again heard fascinating lectures from Casson, both on the
Casson-Gordon work on knots, and more importantly on what are now called Casson handles (Casson called them
flexible handles). These are smooth 4-manifolds that are proper-homotopy equivalent to
open 2-handles, B² X R², and can be smoothly embedded wherever such handles ought to exist were the
Whitney trick to work in dimension 4 the way it does in higher dimensions.

I brought back my handwritten notes on Casson handles (eventually published in [Casson 1986]) and
showed them to Mike; that may have been the start of his seven-year odyssey, ending with his remarkable
work in 1981. Furthermore, his knowledge of the extensions of Casson’s work, done with Bob Edwards
and Larry Siebenmann and appearing in [Casson 1986], enabled him to be the first to realize that there
existed exotic smooth structures on ordinary 4-space, R⁴.

Topological 4-manifolds

Mike became an assistant professor at UC San Diego and published enough to get tenure, but his main
focus was on attempting to prove that Casson handles were smoothly standard. This involved trying to
show that, for example, the n-th Whitehead double of a knot K was smoothly concordant to the
n + 1-st Whitehead double of K for some n. These efforts led to his Reimbedding Theorems, which are a technical
but important part of his future work. After several years, Mike shifted to trying at least to show that
Casson handles were topologically standard, and this he finally achieved with an amazing use of Bing
shrinking techniques.

I recall when Mike announced his results in late August 1981, at a conference at UC San Diego (Dennis
Sullivan was giving a ten-lecture CBMS series). His talk left me very skeptical, and wondering how he
had the nerve to announce such a bombshell with such shaky arguments.
But the experts – Rick Ancel, Bob Edwards, Larry Siebenmann et al. – stayed around after the conference,
and within a week the proof seemed nailed down. It was written up remarkably quickly, by the end of the
year.

Together with Casson’s earlier work, what Mike had done was to show that topological surgery worked in
dimension 4 essentially the same way it worked in higher dimensions, at least for 4-manifolds that were
simply connected or had fundamental groups that did not grow too fast (these were labeled
good groups).

His classification of closed, simply connected 4-manifolds is just beautiful, and is analogous to the
2-dimensional case:

Theorem 1. For each even integer ≤ 2, there exists a unique, orientable, closed surface with that Euler
characteristic.

Theorem 2. For each integral, unimodular, symmetric bilinear form, there exists exactly one
(two, respectively) closed, simply connected 4-dimensional manifold if the form is even (odd, respectively)
with that intersection form.

For example, CP², by having an odd form [1], has a sister, called the Chern manifold
by Mike in honor of Chern’s 70th birthday that year. The pair of sisters, in general, are distinguished in that one has
non-vanishing triangulation (Kirby-Siebenmann) invariant, while the other, vanishing. However, both
manifolds may not be PL.

These manifolds are easy to build, for a form can be used to build a 4-manifold with boundary a homology
3-sphere, and one of Mike’s theorems is that every homology 3-sphere bounds a contractible 4-manifold.

Mike proved an h-cobordism theorem, and from this showed that any 4-manifold proper-homotopy
equivalent to R⁴ was indeed R⁴.

Exotic R⁴‘s

It was March 1982, and Mike was on the phone explaining this amazing theorem of Simon Donaldson
[1983] and how it implied the existence of an exotic smooth structure on R⁴. Mike had been visiting
IHES and had heard a lecture about Simon Donaldson’s Ph.D. thesis by his adviser, Michael Atiyah.
Mike told me that there were these things called “instantons,” certain nice sections of certain complex
2-plane bundles over a 4-manifold X, and that, when the intersection form of X
was positive definite, these instantons formed a moduli space of dimension 5, which was smooth except for cones on
CP², and whose boundary was X. This implied that the intersection form had to be a direct sum of
[1]’s, and that other positive-definite intersection forms were not realized as intersection forms of smooth 4-manifolds.

My immediate reaction was that, c’mon, we don’t make 5-manifolds in that way! But then Mike followed
this up by stating that an exotic smooth structure on R⁴ must exist. He sketched an argument on the
phone which used Donaldson’s result, the work of Casson on “Casson” handles, Mike’s proof that Casson
handles were in fact topologically standard, and a further result of Bob Edwards that these handles lived
in S² X S².

It was most remarkable that R⁴ had an exotic smooth structure, for it had been shown by Stallings [1962]
that in dimensions > 4 there were unique smooth structures, and in dimensions < 4 uniqueness was well known [Moise 1952; Bing 1959; Hamilton 1976]. That dimension four was different was a complete surprise.

I filled in some details to Mike’s sketch and gave some talks about it. Later, probably in summer 1983
during a discussion at tea in Berkeley, Mike remarked that the exotic R⁴ smoothly embedded in
S⁴. I said, it didn’t. After a few rounds of “Yes, it does,” “No, it doesn’t,” we compared constructions.
It turned out that I was using the nonexistence of a smooth, closed 4-manifold with negative-definite
intersection form E₈⊕, whereas Mike needed a compact counterexample to the h-cobordism theorem,
which Donaldson was to produce a year later [1987]. Both examples are written up in [Kirby 1989];
see also [Gompf and Stipsicz 1999] and [Scorpan 2005]. For completeness, I’ll give an outline of my
argument here:

Constructing an exotic R⁴

Start with CP2 with ten points blown up, that is, X⁴ = CP² # 10(-CP²). The intersection form on X is

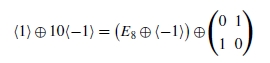
where E₈ is the negative-definite signature -8 bilinear form. Suppose X⁴ is diffeomorphic to Y⁴#S² X S²,
where E₈⊕ [-1] is the negative-definite intersection form of the simply connected smooth 4-manifold Y .
But Donaldson’s thesis [1983] (which Atiyah had described at IHES) ruled out the existence of any such
Y . For he had proved that a smooth, negative-definite, simply connected, closed 4-manifold must have
intersection form equal to ⊕ n(-1). Thus, X does not smoothly split off an S² X S².

However, in spring 1974 at IHES, Casson had lectured on his development of Casson handles, namely,
smooth 4-manifolds pairs (H ∂ H), which were proper-homotopy equivalent to B² X B², S¹ X B², with ∂ H diffeomorphic to
S¹ X R². Casson showed [1986] that whenever the homotopy-theoretic conditions
implied (if we were in higher dimensions) that there would exist an embedded smooth 2-handle, then,
in dimension 4, a smooth Casson handle could be embedded. In particular, two Casson handles could
be attached to a 0-handle such that the resulting interior is an open 4-manifold M proper-homotopy
equivalent to S² X S² – {q} for some point q. Then, M could be smoothly embedded in X to represent
the hyperbolic summand of the intersection form on X.

After hearing Casson’s lectures, Bob Edwards showed an important additional fact about Casson handles,
namely that H was also diffeomorphic, rel boundary, to a standard 2-handle B² X B² minus the cone
(into the interior of B² X B² on a generalized Whitehead continuum Wh embedded in B² X S¹. Thus,
M⁴ is a smooth submanifold of S² X S², as well as of X.

Then, in 1981 Freedman showed [1982] that Casson handles were topologically standard, meaning that
the diffeomorphism from ∂H to S¹ X B² extended to a homeomorphism from H to B² X B². It follows
that M is homeomorphic to S² X S² – {q}, and that X topologically splits off an S² X S², leaving a
closed 4-manifold Y‘ that cannot have a smooth structure.

The exotic R⁴ arises as the complement of the topologically embedded S² ^ S² given by the cores of
the 0-handle and two Casson handles in S² X S² (as realized by Edwards in the paragraph above). This
complement is smooth (as an open subset of S² X S²), is easily seen to be proper-homotopy equivalent
to R⁴, and is then homeomorphic to R⁴ by Freedman. Call this complement R⁴_Σ, with Σ denoting the
smooth structure.

Suppose that R⁴_Σ were diffeomorphic to R⁴. Then, it would have smoothly embedded S³‘s outside any
compact subset. In particular, there would be a smoothly embedded S³ close enough to the wedge
S²^S² so that the S³ lay smoothly inside M, and thus smoothly inside M – now thought of as a smooth
submanifold of X and representing the hyperbolic pair in the intersection form.

Now, cut X along this smooth S³, throw away the part lying in M, and smoothly glue-in B⁴. This
smoothly splits off the hyperbolic pair, leaving a simply connected 4-manifold with negative-definite
intersection form, contradicting Donaldson’s theorem. Thus, R⁴_Σ is not diffeomorphic to R⁴.

For a while, some theoretical physicists wondered whether an exotic R⁴ might underlie our universe, but
then it was seen that these exotic R⁴‘s were really strange 4-manifolds; what was weird was that they
were homeomorphic to standard R⁴.

Fairly soon, Bob Gompf [1983] had produced a few more exotic R⁴‘s. Eventually, there were uncountably
many [Taubes 1987] (these are most easily thought of as all the open 4-balls of any radius bigger than a
given constant, with the smooth structures inherited as open sets of one big exotic R⁴).

It is possible that all compact topological 4-manifolds have countably many smooth structures, and that
all non-compact ones have uncountably many smooth structures.

Awards

For a while, Mike may have been the most highly decorated young mathematician.

• 1984: Elected to US National Academy of Sciences
• 1984: California Scientist of the Year
• 1984-1989: MacArthur Foundation Fellow
• 1986: Veblen Prize in Geometry, AMS
• 1986: Fields Medal
• 1987: National Medal of Science (US)

These awards go to, at most, a few mathematicians per year.

There are various ways to measure the quality of a paper or body of work. One way is to assume the
individual had not done the work and try to guess how long afterwards the work would have been done
by someone else. In Mike’s case, I could guess that his theorems on topological 4-manifolds would still
not have been carried out, even thirty years later, as this is written.

There is no photo of Mike receiving the National Medal of Science from the President, for, as Mike’s
father, Ben, recollects:

When Mike received the notification from the White House that he had won the National Medal
of Science, he showed it to us. Nancy said we’d fly there with him; it was a high point in our
lives. Mike said he was thinking of not going. His first son was just born, and he didn’t want to
leave him. Also, he was close to a breakthrough on a big problem. Third, he didn’t really enjoy
honors and medals and shaking hands with presidents. So we went, Reagan shook my hand,
and we celebrated with Raoul Bott, who was also a Medalist.

The in-between years, 1982-1997

In the mid 1980s I remember Mike saying that, with all those awards, especially the Fields Medal, he
needed to not only produce research but look like a real mathematician, so he intended to fill in some
of the gaps in his knowledge of mathematics due to his abbreviated years in school and his focus on
4-manifolds. He did so remarkably well, in my opinion, but at the same time continued his work in
low-dimensional topology.

Whether or not Mike’s work on 4-manifolds covered all fundamental groups, or just the good ones, led to
what is called the A-B-slice problem, which Slava Krushkal summarizes in his commentary on those
papers. Mike and Slava are currently skeptical that all groups are good.

A quantum computer

In the fall of 1988, Mike visited Harvard on sabbatical. At that time, Witten’s preprint [1989] on quantum
field theory and the Jones polynomial had appeared, and Raoul Bott and Cliff Taubes organized a seminar
centered on the preprint. Although the preprint had no mention of framings on links, which was sorted
out soon, Mike thought the paper was revolutionary and that quantum field theory was a powerful tool.

It had also been shown [Jaeger et al. 1990] that computing the values of the Jones polynomial is #P-hard,
that is, it belongs to the class of NP problems where, instead of asking whether there is a solution, it asks
how many solutions. This led Mike to think about building a quantum computer to solve these problems;
as he wrote later [1998],

Non-abelian topological quantum field theories exhibit the mathematical features necessary
to support a model capable of solving all #P problems, a computationally intractable class, in
polynomial time. Specifically, Witten [1989] has identified expectation values in a certain SU(2)
field theory with values of the Jones polynomial that are #P-hard. This suggests that some
physical system whose effective Lagrangian contains a non-abelian topological term might be
manipulated to serve as an analog computer capable of solving NP- or even #P-hard problems
in polynomial time. Defining such a system and addressing the accuracy issues inherent in
preparation and measurement is a major unsolved problem.

Mike was barking up the wrong physics tree for a while. Knowing SU(2) was associated to the weak
force, he presumed some kind of nuclear physics would be required to build a quantum computer. He
only learned around 1995-96 about a paper of Greg Moore and Nicholas Read [1991] in which “the
modern techniques of two-dimensional conformal field theory are applied to the theory of the fractional
quantum Hall effect.” This paper shows that the “effective” low-energy field theory might be an SU.2/
gauge theory. Since 2005, Mike’s research unit has been supporting experimental work at numerous
locations around the world, to explore topological phases of matter. Much of this research has been on
the fractional quantum Hall effect, and on Majorana systems built from semiconductor/superconductor
interfaces.

Microsoft and Station Q

Mike felt his research focus was changing, and that it was not a good idea for him to train graduate
students in areas where he was a beginner himself. When he visited Microsoft in 1996 to give a talk,
Nathan Myhrvold, Chief Technology Officer at Microsoft, offered him a job on the spot. This seemed a
good fit for Mike’s new interests, and he left UC San Diego for Microsoft in July 1997.
He convinced Microsoft to open a research group, called Station Q, on the UC Santa Barbara campus on
15 March 2005. The original group included Chetan Nayak, Alexei Kitaev, Kevin Walker, and Zhenghan
Wang, and has expanded since.

When I asked Mike about favorite papers outside 4-manifold theory, his immediate response was his
paper with Danny Calegari and Kevin Walker [2010] on the positivity of universal pairings in dimension 3.
Kevin gives his perspective on this work in his commentary.

Miscellany

For a while in the 1980s, Mike worked summers for ‘JASON,’ an independent group of younger scientists
chosen to advise the US government in out-of-the-ordinary ways. It was established in 1960, funded
through the MITRE Corporation, and included distinguished scientists (e.g., Freeman Dyson, Sidney
Drell, Walter Munk, Richard Muller, and Marshall Rosenbluth).

While there, Mike had an idea, perhaps too out of the ordinary even for JASON, which was to offer US
statehood to Panama, Kuwait and Israel; they would get security and various benefits of being a part of
the US, and the US would get in return the Panama Canal, oil, and brains. Well, it would never actually
happen, but the story is that Sid Drell mentioned it to then-Secretary of State George Shultz over dinner,
but without mentioning Mike’s name so as to save his reputation! A version of this idea, titled “A proposal
on Panama”, can be read from Mike’s bibliography on this site.
In addition, Mike has tried his hand at writing vignettes from his early “adventures”, also listed as “Night
climbing” and “Jon Loni’s Stoney Point massacre: A story twice retold”. Both are available here as well.

References

[Bing 1959] R. H. Bing, “An alternative proof that 3-manifolds can be triangulated”, Ann. of Math. .2/ 69 (1959), 37-65. MR 20
#7269 Zbl 0106.16604

[Calegari et al. 2010] D. Calegari, M. H. Freedman, and K. Walker, “Positivity of the universal pairing in 3 dimensions”, J. Amer.
Math. Soc. 23:1 (2010), 107-188. MR 2011k:57037 Zbl 1201.57024

[Casson 1986] A. J. Casson, “Three lectures on new-infinite constructions in 4-dimensional manifolds”, pp. 201-244 in À
la recherche de la topologie perdue, Progr. Math. 62, Birkhäuser, Boston, MA, 1986. With an appendix by L. Siebenmann.
MR 900253

[Donaldson 1983] S. K. Donaldson, “An application of gauge theory to four-dimensional topology”, J. Differential Geom. 18:2
(1983), 279-315. MR 85c:57015 Zbl 0507.57010

[Donaldson 1987] S. K. Donaldson, “Irrationality and the h-cobordism conjecture”, J. Differential Geom. 26:1 (1987), 141-168.
MR 88j:57035 Zbl 0631.57010

[Freedman 1982] M. H. Freedman, “The topology of four-dimensional manifolds”, J. Differential Geom. 17:3 (1982), 357-453.
MR 84b:57006 Zbl 0528.570

[Freedman 1998] M. H. Freedman, “P/NP, and the quantum field computer”, Proc. Natl. Acad. Sci. USA 95:1 (1998), 98-101.
MR 99b:68064 Zbl 0895.68053

[Freedman and Kirby 1978] M. Freedman and R. Kirby, “A geometric proof of Rochlin’s theorem”, pp. 85-97 in Algebraic and
geometric topology (Stanford, CA, 1976), Part 2, Proc. Sympos. Pure Math. XXXII, Amer. Math. Soc., Providence, R.I., 1978.
MR 80f:57015 Zbl 0392.57018

[Gompf 1983] R. E. Gompf, “Three exotic R⁴‘s and other anomalies”, J. Differential Geom. 18:2 (1983), 317-328. MR 85b:
57038 Zbl 0496.57007

[Gompf and Stipsicz 1999] R. E. Gompf and A. I. Stipsicz, 4-manifolds and Kirby calculus, Graduate Studies in Mathematics
20, American Mathematical Society, Providence, RI, 1999. MR 2000h:57038 Zbl 0933.57020

[Hamilton 1976] A. J. S. Hamilton, “The triangulation of 3-manifolds”, Quart. J. Math. Oxford Ser. .2/ 27:105 (1976), 63-70.
MR 53 #11618 Zbl 0318.57003

[Jaeger et al. 1990] F. Jaeger, D. L. Vertigan, and D. J. A. Welsh, “On the computational complexity of the Jones and Tutte
polynomials”, Math. Proc. Cambridge Philos. Soc. 108:1 (1990), 35-53. MR 91h:05038 Zbl 0747.57006

[Kirby 1989] R. C. Kirby, The topology of 4-manifolds, Lecture Notes in Mathematics 1374, Springer, Berlin, 1989. MR 90j:
57012 Zbl 0668.57001

[Moise 1952] E. E. Moise, “Affine structures in 3-manifolds. V. The triangulation theorem and Hauptvermutung”, Ann. of Math.
.2/ 56 (1952), 96-114. MR 14,72d Zbl 0048.17102

[Moore and Read 1991] G. Moore and N. Read, “Nonabelions in the fractional quantum Hall effect”, Nuclear Phys. B 360:2-3
(1991), 362-396. MR 92j:81291

[Scorpan 2005] A. Scorpan, The wild world of 4-manifolds, American Mathematical Society, Providence, RI, 2005. MR 2006h:
57018 Zbl 1075.57001

[Stallings 1962] J. Stallings, “The piecewise-linear structure of Euclidean space”, Proc. Cambridge Philos. Soc. 58 (1962),
481-488. MR 26 #6945 Zbl 0107.40203

[Taubes 1987] C. H. Taubes, “Gauge theory on asymptotically periodic 4-manifolds”, J. Differential Geom. 25:3 (1987), 363-430.
MR 88g:58176 Zbl 0615.57009

[Witten 1989] E. Witten, “Quantum field theory and the Jones polynomial”, Comm. Math. Phys. 121:3 (1989), 351-399.
MR 90h:57009 Zbl 0667.57005